Page Contents
WHAT IS MOMENT OF INERTIA?
Inertia is a property of a body under which it continues to be in a state of rest or uniform motion until it is acted upon by an external force.
Now, this can be said for a body in a linear motion. But what if the body is in a rotating motion? The resistance offered to the angular acceleration by a rotating body is called Moment of inertia (or) Mass moment of inertia.
Is this the parameter which is widely used in structural engineering as “I“? The answer is NO!
The moment of inertia represented by “I” and used in deflection calculations of a beam, buckling load calculations of a column and in many other places in structural engineering has nothing related to the terms Mass or Inertia.
So what is this “I” which is used all over in structural application? It is the Area Moment of Inertia or Second Moment of Area.
WHAT IS AREA MOMENT OF INERTIA (I)?

Quick Answer: It is just a name that we gave to stiffness due to the shape of an element. Like, Young’s modulus is a stiffness due to material it is made of.
It can be defined as the resistance offered by a cross-sectional area to bending. It is completely independent of the mass and other mechanical properties of the body. It can be explained by a simple illustration.
In the picture shown, the cross-section of the plank is the same in both cases. Also, same beam, same area, same Young’s Modulus. The only thing that changes is its geometry.
It can be seen that bending is low in case 1 compared to case 2. This is because the beam 1 has a higher area moment of inertia about the bending axis compared to the beam 2.

As you can see the area of the beam cross-section 1 is concentrated more away from the bending axis than in the beam 2. Hence the beam 1 has a higher Area moment of inertia.
Thus, more the distance of the area from the bending axis higher is its area moment of inertia. This is the major reason why sections shaped like an “I” is preferred over the rectangular cross-section.
An I – section has a larger area concentration away from the centroidal axis compared to a rectangular cross-section of the same area as shown.
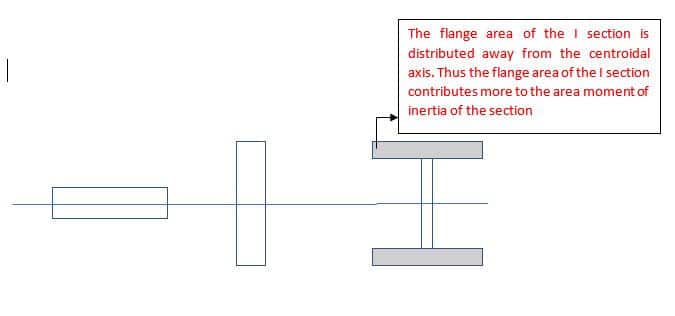
From the above image, it can be easily understood that an I section has a higher value of area moment of inertia compared to the rectangular section of the same cross-sectional area. And the reason is it has its area distributed away from the centroidal axis.
HOW IS AREA MOMENT OF INERTIA CALCULATED?
Now that we have understood how a distributed area influences the value of I, we shall see about how exactly area moment of inertia of a section is calculated.
Area moment of inertia is also known as the second moment of an area for a reason. It can be calculated by taking moment about the area twice i.e.,
Second moment of area = (area) x (perpendicular distance)2.

The perpendicular distance depends on the axis of bending. The following are the generalised formula for area moment of inertia.
$$I_x=∫y^2 \>dA $$
where dA = area in consideration, y = perpendicular distance taken from X-axis. As the reference axis is considered as X-axis, the moment of inertia thus calculated is.
$$I_y=∫x^2 \>dA$$
where x = perpendicular distance considered from Y-axis.
Unit of I is units4 i.e., mm4, in4, m4.
POLAR MOMENT OF INERTIA (J)
Similar to I, Polar moment of inertia (J) represents the resistance of the shape of the cross-section. While I represents resistance to bending, J represents resistance to twisting about the reference axis. From the perpendicular axis theorem, J can be calculated as the sum of Ix and Iy.
Significance of Area Moment of Inertia
- It is a cross-sectional property that can be used to predict the resistance of beams to bending and deflection.
- It plays a major role in selecting and sizing the type of cross-sections to be used as flexural members in a structure.
- It is used in calculating Bending Stresses.
- It is used in Analysis of Beams and Columns.
- It is also used in calculating critical buckling load of a column and flexural rigidity.
IMPORTANT POINTS
- Some Cross-sections are efficient at resisting bending than others. The further the material spreads away from the bending axis, the stiffer a cross-section tends to be.
- It is not a unique property of cross-section. Its value changes depending on the place of reference axis.
- I is nothing but stiffness due to the shape of the material.
- Similar to stress, I is also a tensor quantity. Hence, all rules of transformation can be applicable.
