A staircase is a component of a structure which provides access to different levels of the structure and also serves as an emergency escape route in case of a fire. We shall learn how to design a staircase manually. To learn how to design, we need to know different components of it.
There are various types of staircases used in structure based on their functionality and space available for construction.
The following some of the important types of stairs generally used in structures
1. Geometric Stair
2. Quarter turn stair
3. Bifurcated stair
4. Circular stair
5. Spiral stair
6. Open newel stair
7. Dog legged stair
8. Straight stair
Dog legged staircase is the most commonly seen and economical staircase. These stairs are arranged with two adjacent flights running parallel with a mid-landing. Where space is less, the dog-legged staircase is generally provided resulting in economical utilization of available space. In this post, we shall discuss the structural design of a dog-legged staircase.
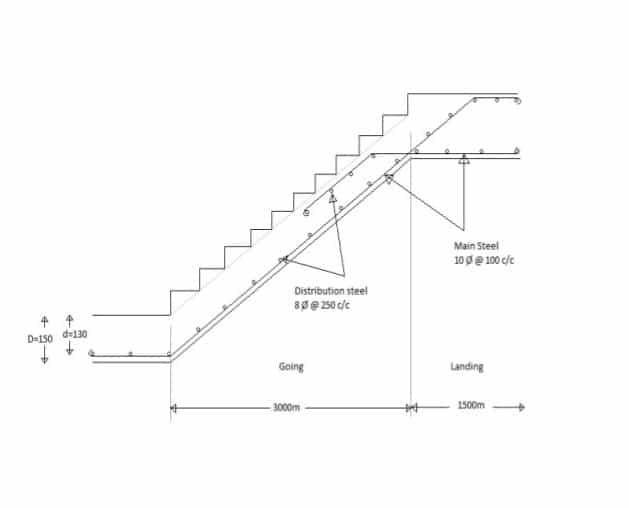
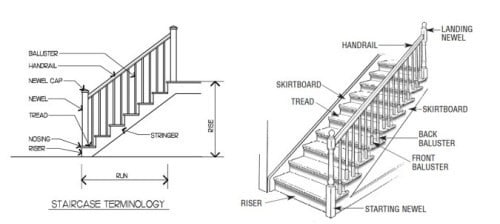
The staircase consists of steps with Landings. The flight of steps is called Going. The number of steps in one Going depends on the Rise (i.e., the vertical distance between two steps) and the Tread (i.e., the width of the step).
RISE AND TREAD
Rise and Tread depend on the importance and functionality of the building. In Public buildings, Rise is about 15 cm and in Residential buildings, it may vary from 15 cm to 18 cm. The Tread in Public buildings is taken about 30 cm and in Residential buildings, it may vary from 20 to 30 cm. The sum of Tread and twice the Rise is about 60 cm.
EFFECTIVE SPAN
As per clause 33.1 (b) of IS 456
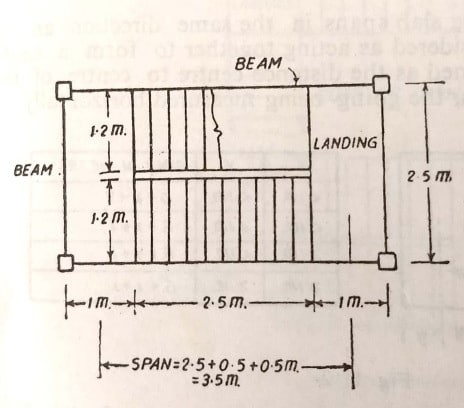
The effective span of stairs supported at each end by Landings is taken as a distance equal to the Going of the Stairs + Z.
Z can be calculated as mentioned below.
If X be the half-width of a landing at one end and Y be the half-width of landing at the other end of the Going as shown below then,
Z = X + Y, provided X and Y cannot be greater than 1 m.

DESIGN A STAIRCASE
The following are the design steps to be followed for the structural design of a staircase and it is illustrated by a typical example.
Step 1 Determine the Height of each flight
It is calculated by dividing the total storey height by the number of flights. In this case, the storey height is taken as 3.2 m and a number of flights are 2. Hence the height of each flight is 1.6 m.
Step 2 Determine the Width of each flight
In this example, the overall width available is 2.5 m. A 100 mm gap is given in between the two flights and hence width of each flight would be 1.2 m.
Step 3 Calculation of Number of Riser and Tread
Assuming Riser as 160 mm and Tread as 250 mm,
No of Risers=(Total Height of each flight)/(Height of each Riser)
No.of Treads=No.of Risers-1
On calculating, we get, No. of Risers is 10 and No. of Treads is 9.
Step 4 Assume the Thickness of Waist slab
Generally, the thickness of the waist slab is assumed between $\frac{L}{20}$ to $\frac{L}{25}$ where L is the effective span of the staircase which can be calculated as per the IS guideline explained above.
Here, Effective Span = 3.5 m
Step 5 Calculate the total load on the staircase
Total load on the stair = Dead load + Live Load + Floor Finish
where
DL = Weight of Steps + Weight of waist slab
LL = generally taken between 3 kN/m2 to 5 kN/m2
FF= generally takes as 0.8 kN/m2 to 1 kN/m2
On the landing area, the weight of steps is not included in the total load.
Step 6 Find the maximum Bending Moment
Now from the loading, the reaction at each end support is calculated using the basic equilibrium equations. With reactions and load values, the maximum Bending Moment (BM) can be calculated. Using this maximum BM, the minimum depth required is calculated as follows
$$M_{ulim} = 0.36\times \frac{x_{umax}}{d} \times (1-\frac{0.42 \times x_{umax}}{d}) \times f_{ck} bd^2$$
$$d_{min} =?$$
If the calculated minimum depth is less than the assumed thickness of the waist slab then the design is safe. Otherwise, a greater depth has to be assumed and the steps need to be repeated.
Step 7 Reinforcement Details
The area of main reinforcement required is calculated as follows
$$P_t=(\frac{50f_{ck}}{f_y})\times(1-\sqrt{1-\frac{4.6M_u}{f_{ck}bd^2}} )$$
$$A_{st}=\frac{P_t}{100}\times bd$$
where Ast = Area of steel required and Pt = Percentage of steel required
The calculated Ast is provided as the main reinforcement and minimum reinforcement of 0.12 % is provided as distribution steel in the other direction.
An example of reinforcement detailing of a dog-legged staircase is shown below