Stress Transformation and Mohr’s Circle

Introduction

German physicist Otto Mohr developed a method to graphically interpret the general state of stress at a point. This method is named as Mohr’s circle and can be used to evaluate principal stress, maximum shear stresses and normal and tangential stresses at any plane.

Let us take up a simple 2D stress element to understand about the concept of stress transformation and how Mohr’s circle can be used to simplify the process.

Stress Element

A stress element is a useful way to describe the stresses acting at a single point within the body. Let us consider a simple example of the beam with axial load. now the stress state in the stress element will be very simple. It will only have normal stress along X-axis and zero normal stress along Y-axis and zero shear stress. If we rotate the stress element to get the stress state for a specific angle. Depending on how we orient the stress element we will get different values for normal and shear stress components.

The normal and shear stress for the stress element oriented in a specific angle (or in other words an inclined plane) by using the Stress Transformation Equations.

Stress Transformation Equation

The following are the stress transformation equations,

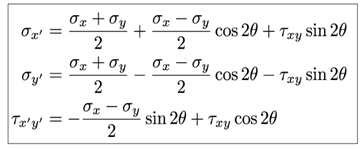
The inputs for these equations are normal stresses σ_x,σ_y and shear stress τ_xy at the starting element orientation and θ is the angle the stress element to be rotated or the inclination of a plane at which we need normal and shear stresses.

As the stress element rotates, the normal and shear stress will vary and this variation can be easily understood with an example.

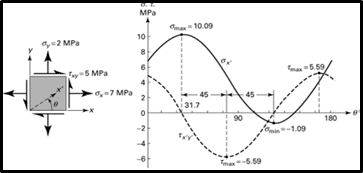
From this example, it can be observed that once the element rotates 180 degree, the values of normal and shear stress comes to the original position. Remember, the actual state of stress applied to the body is not changing when the element is rotated.

Observations from the graph

1. At certain angles, the normal stress curve reaches a maximum and minimum values and these values are separated by an angle of 90 degrees.
2. This means that at a particular angle of rotation when we get maximum normal stress at one face (say X face) then the minimum stress will be perpendicular to that face (at Y face).
3. Whenever the normal stress curve reaches maximum or minimum value, the shear stress at that angle will be zero.

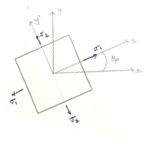
We know that the plane at which the shear stresses are zero, that plane is known as Principal Plane and the corresponding normal is Principal Stresses (σ₁, σ₂). The rotation angle of the principal plane is denoted as θp.

Mohr’s Circle

It is a graphical method for easily determining normal and shear stresses “WITHOUT” using the stress transformation equations.

Mohr’s circle is drawn on a 2D graph where normal stress is taken on the horizontal axis and shear stress is taken on the vertical axis.

Sign Convention

If the shear stresses tend to rotate in anti-clockwise direction are taken as positive and shear stresses tends to rotate in clockwise direction are negative. That’s why the shear stresses in Y-face are taken as negative. So, positive shear stresses are plotted on downward direction and negative shear stresses on upward direction.

Normal stresses tensile in nature are positive and compressive in nature are negative.

Steps to Draw Mohr’s Circle

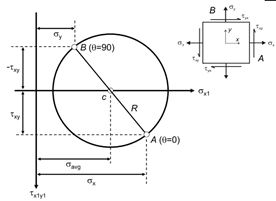
1. Set the coordinate axis (σ – X-axis, τ – Y-axis)
2. Plot the points A (σ_x,τ_xy) and B (σ_y,-τ_xy).
3. With A and B as diameter and C as the centre, draw a circle.

Note that at point A, θ=0 degree and at B, θ=90 degree.

i) Double Angle Method

Stress Transformation using Mohr’s Circle

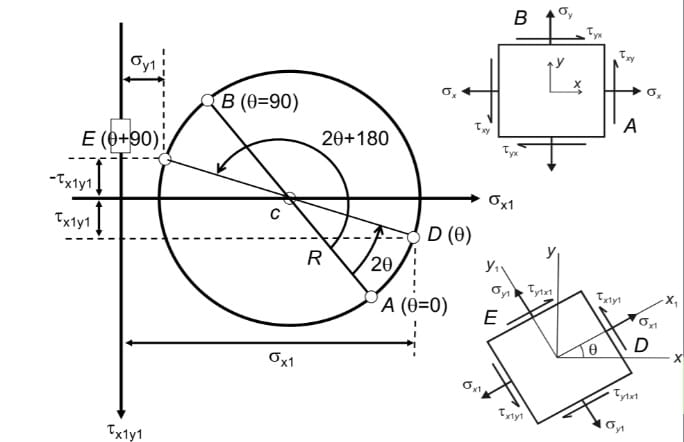
Let us assume that we need normal and shear stress on a plane inclined at an angle θ. In Mohr’s circle both σ_x and σ_y are marked in a same axis (i.e., 180 degree) which is not a real case as σ_x and σ_y are perpendicular to each other (i.e., 90 degrees).

Therefore, with CA as reference locate the point D on the circle at an angle 2θ. Locate another point E diametrically opposite to D. The X coordinates of D and E represents the normal stresses on x and y faces respectively and the Y coordinate represents the shear stress on the new inclined plane.

Principal Stresses

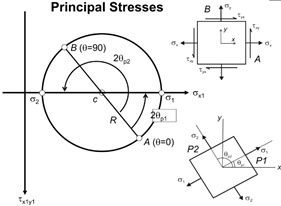
Principal stresses act on the principal surface/plane at which the shear stress is zero. The horizontal axis of the Mohr’s circle the value of shear stress will always be zero. Hence, the points at which the horizontal axis cuts the circle gives the Maximum and Minimum principal stresses. The angle between the CA and horizontal axis is 2θp from which the inclination of principal plane (θp) can be calculated.

Maximum Shear Stress

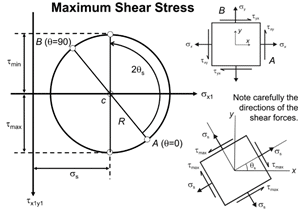
Visually it can be observed that the extreme points of the circle in vertical axis gives the maximum shear stress. Geometrically, maximum shear stress is nothing but the Radius of the Mohr’s circle.

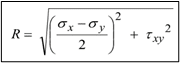
The Angle between CA to the vertical is 2θs and θs is the inclination of a plane at which the maximum shear stress will occur.

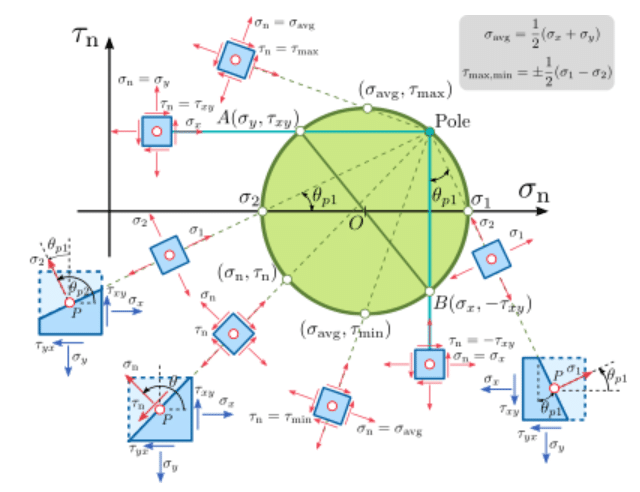
ii) Pole Method:

What is a pole?

Pole method is based on a unique point on the Mohr’s circle known as the Pole. This pole is unique, because any strainght line drawn through the pole intersects the Mohr’s circle at a point representing the state of stress on a plane with the same orientation as the line. As shown in the figure, a line drawn through the pole and some stress point (σ,τ) on the circle is exactly parallel to the plane with corresponding σ and τ, making this approach very intuitive.

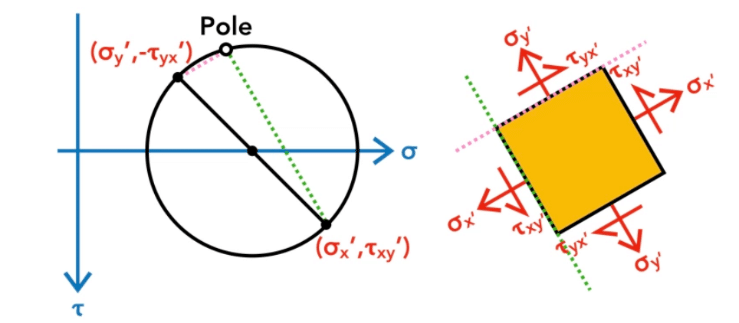
How to locate Pole?

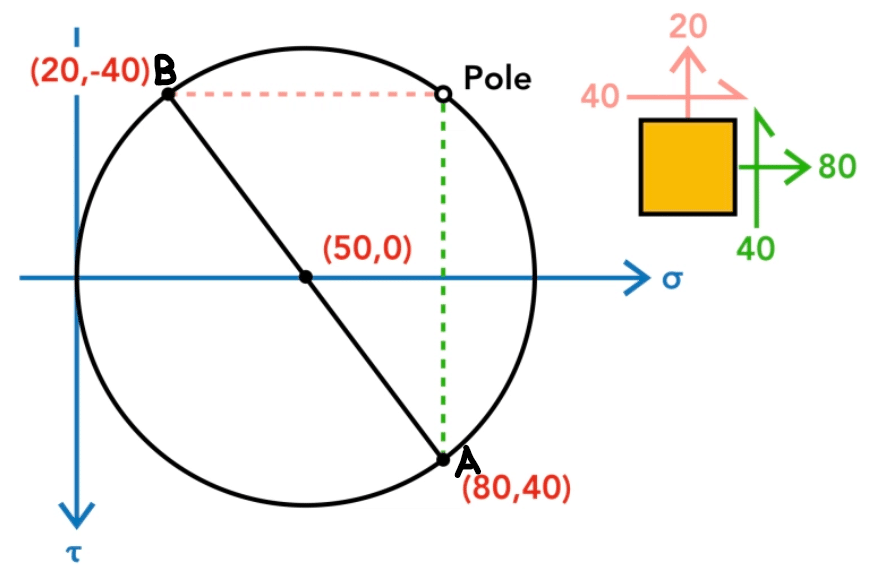
Let us locate the pole in Mohr’s circle with an example. The figure shows the stress state on an element and its Mohr’s circle.

To locate the pole, From point A draw a line parallel to X face (green) and from B draw a line parallel to Y face (red). These two points will intersect at a point on the circle and this point is called Pole.

Stress Transformation and Principal Stresses:

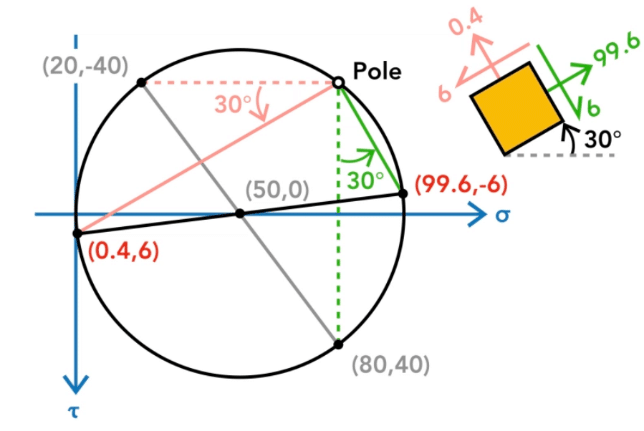
For example, let us calculate normal and shear stresses for an element rotated for an angle 30 deg in anti-clockwise direction. To locate the stress state for the inclines plane, draw two lines from pole with an angle 30 deg anti-clockwise from green and red lines. These lines will be parallel to the X and Y faces of the rotated element respectively. The coordinates of the points at which these lines intersect the circle will give the stress state of that plane.

Similarly, the angle of Principal plane can be calculated by connecting the pole with the σ₁ and σ₂.

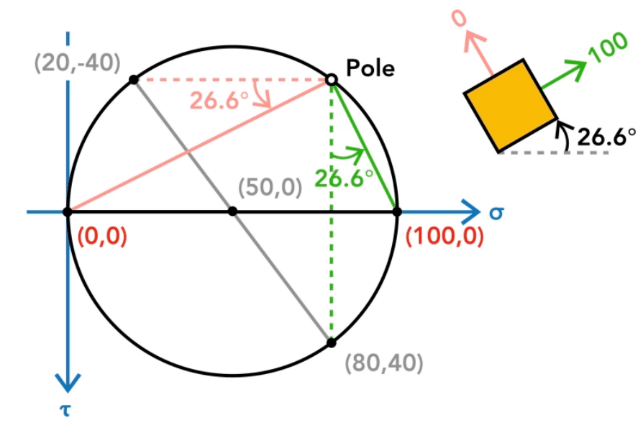
The following figure shows how pole can be used to calculate normal and shear stress for different orientation of stress element.